One of the methods of vectorization of similar goods names. Сase of heavy loaded identification.
Introduction
Suppose you are an organization that receives statistics on purchases of various and numerous shops that are not organized in a unified network. Each store has its own database of goods. Each of this stores has it’s own ideas about the products titles.
Someone thinks that it is enough to name the potatoes like this – “Farmer’s potatoes 1 kg.”, and someone — “Farmer’s fresh potatoes, young big yellow 1000g.” However, in fact it is one and the same product from the same farm.
Quite an interesting question arises — is it possible to combine all similar products from different shops, to examine, for example, the total flow of goods and other interesting metrics.
It’s clear, that there is no way this can be made without mistakes, but certain steps in the direction of goods unification can be made. I will tell about some of this steps.
This project was carried out within the framework of the work performed by Maxilect company, other projects of this category can be viewed here.
Technical features
Features of this problem are determined by technical subtasks into which the business problem divides:
- Formation of clusters of unified names;
- Identification of unified names (classification);
- Effective processing of a large number of goods titles.
Thus, the final solution must on one hand be technically efficient, but on the other — spend very little time to the process one product title. At this point we drop a large list of useful techniques that works well with small samples. For instance, standard Python libraries for data processing.
If we have a load of 1 million products per hour, at least 300 names of the goods must be processed in one second. However, the load at different times of the day varies greatly, thus the required speed rises to 1000 names per second. Building of the vectorization with dimension of 100 000, usage of word2vec, deep learning, cluster models of gigabytes size, … — it’s not about us. The task itself is not important enough (for business) to allocate hundreds of servers that will work with accurate but computationally expensive methods.
Thus, the technical side of the problem takes the following formulation:
How to choose an extremely economical vectorization of text, which would allow relatively effectively deal with the problem of clustering and classification and use very simple methods(for speed)?
After a time of creative torment we have come to such an option.
Vectorization
At first (and only once) we form a dictionary of indices of used alphabet and numerals of length M:
| a | b | c | d | … |
| 1 | 2 | 3 | 4 | … |
Exact numbers in index are of no fundamental importance.
Further, every word in the product title is truncated to N letters. The matrix V (initially zero) size of MxN values are calculated in accordance with the formula:
,
where j — index of letter in the word, W — all words in title, wj-th— j-th character in the word, i — the dictionary index of j-th character, and f(j,wj,i) a function of the weights, depending on the letters, places of the letters in the word numbers, letters dictionary index. Logarithm was selected from empirical considerations, as it showed the best result.
Weight function f(j,wj,i) can be, for example, an exponentially decreasing with j as parameter. In our case, as the weight function a list of weights was used for the first 12 letters. Exact weights were chosen empirically. All indexes in the dictionary were assumed equivalent.
Example:
Suppose we have a product “abc cd”, with obvious indices [1,2,3] [3,4] and piecewise linear function of decreasing significance to the letters in the word with values – f([1,2,3, 4,5,6, …]) = [80, 60, 40, 20, 0.0, …].
Then the matrix V will be:
| 80 | 0 | 80 | 0 | … |
| 0 | 60 | 0 | 60 | … |
| 0 | 0 | 40 | 0 | … |
| … | … | … | … | … |
Matrix form is used to count “key” of the title. The key name is calculated as follows:
,
where V1- the first row of the matrix V, and Idx(V1>0)- a function that finds the indices of all the non-zero letters.
In some aspects, this vectorization is inspired by Jaro-Winkler similarity. Namely, with the presence of the prefix in the word and high significance of the first letters.
Clustering
Clustering that is described here is quite simple. It’s a trivial algorithm for unsupervised learning. However, nothing prevents from using something more sophisticated. This one is only used because of the speed and simplicity. Its main feature is that it should create a large amount of small clusters and the number of these clusters is not known in advance.
Algorithm input: V – unclassified vectorization of the product name, K – key of this vectorization , Model – Dictionary, clustering model.
Algorithm itself:
1. Model = dict ()
2. For all vectorized product names V with key K
a. If K not in the Model.keys:
i. Create a new cluster C with the center V
ii. Add C to a new list Model[K]
b. Otherwise:
i. For each cluster in Model[K]:
1. Select the closest cluster to V
2. If all the clusters are too far, create new and add to the Model[K]
3. If you have a close cluster, add new element V to it and recalculate the center of the cluster
3. Return Model
Matrix is flattened during the “training”, because their properties are needed only at the stage of key calculation. The similarity is estimated by the cosine measure (several has been tested and this has given the best result). Algorithm has a parametric cluster boundary. If the vector is away from the cluster center to the extent greater than a certain number, it is stated that it is a different cluster.
There is several problems in this implementation. During the displacement of the cluster center some of the cluster elements can become closer to the neighboring clusters. However, search for an cluster equilibrium can “eat” a lot of the neighboring elements and combine a lot of objects into a single cluster.
The alternative is a simple — “no center recalculation”. Paragraph (1.b.i.3) is simply ignored. In general, clusterization doesn’t go bad enough in this situation to regret it.
Classification
Training is a quite isolated from the “process” in the organization. You can let the server to train for a week, and then implement the model. And do so once a month. However, classification, according to the trained model, must be quick and process a lot of information in a short time.
In this case, the main shamanic dance with a tambourine occurs around the keys, which do not necessarily coincide with a input name key, but might be alike.
At the input of the algorithm: V – unclassified vectorization of the product name, K – key to this vectorization(here it is important that this is a set), Model – clustering model, Applicants – the list of keys of lists which can possess the right cluster, CSD – limiting constant, Sym_diff () – a function of the symmetric difference.
The algorithm:
1. Applicants = []
2. If K is in Model.keys:
a. The K is added to Applicants
3. Otherwise:
a. For each MK in keys:
i. Sd = Sym_diff (MK,K)
ii. If len(Sd) <CSD:
1. MK is added to the Applicants
4. For each cluster from each list with the keys from the Applicants:
a. Select the closest cluster to V
b. If all the clusters are too far away, we return an empty element
c. If there are close clusters, return the nearest of them
Algorithm checks the similarity with cosine measure, and has boundary parameter which tells us that some good title does not belong to some cluster.
Testing
The most expressive test, this test is one which was not invented by us.
At the point of a deep satisfaction with our work at an earlier algorithm version, when the original test data showed us only double-digits with a number 9 on the right place, came a test sample from outside. And then, suddenly, the percentage of recognition accuracy has fallen to something accross 60%. This, however, wasn’t too bad, because the people who gave us this sample had a correct recognition score around 40%. Nevertheless, this event caused as a deep sense which was of the opposite to the initial and gave us a desire to rethink our lives. The result of this rethinking is the current algorithm and test results are displayed for it.
The two main parameters which can be varied in the classification are:
- distance range — a distance restriction, that tells us that certain vectorization doesn’t belong the the certain cluster;
- cut length — the upper limit for the inclusion of a list of clusters into the “applicants”.
Of course, increasing the cut length can highly increase the number of the “applicants” clusters. This is not very good for the classification speed. However, this decreases the number of clusters, which were ignored, because their keys were not found in model.
We measured the performance of algorithm for a table of 20×20 controlled parameters to see what happens.
- The test sample contains 923 combinations of the real names of the goods and the “right” product names.
- The model was trained on all the unique product names from the “right” side of the initial sample.
- If the unified name is not found in the model, the output is a an empty set. If found, but incorrect, the False output. If properly found — True.
- Further, these data are aggregated in the number of classified, the number of correctly and incorrectly classified.
That’s what happens with the percentage of goods for which the classification was found(doesn’t matter correct or incorrect).
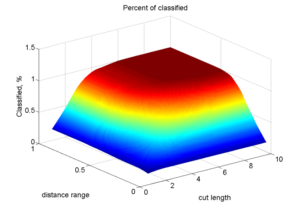
Reducing of the distance range to values less than 0.5 and the cut length to a values less than 4 leads to a sharp reduction in the amount of detected products. If both these values are exceeded, the algorithm reaches a plateau with 100% recognition (which, incidentally, may not always be good in theory).
First figure shows quite obvious relationship, because both of parameters contribute to the amount of ignored clusters.
Detection efficiency is a little more interesting. Dependence of the number of incorrectly recognized by these two parameters looks quite unusual.
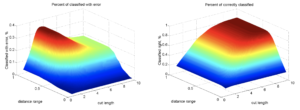
Hump on the cut length from 2 to 4 corresponds to a sharp increase in the number of “applicants” clusters lists. In case of a large enough distance range, the lists of candidates is too big. In this case, when the amount of “applicants” is growing the probability of finding the “real” name as the minimum increases, so hump starts to drop to 17% from 34%.
Finally, and most importantly — a recognition rate. At first it may seem surprising that in this figure, there is no hump. However, then we remember that the percentage of incorrectly recognized is relative to the “all recognized”, and the number of them increases monotonically with an increase in both parameters. The percentage of correctly recognized is in relation to the entire sample, not only “all recognized”.
Small conclusion
Ultimately, we have achieved acceptable results for external data sample. 83% correct recognition and quite fast speed. For the problem with a sufficiently large variation of “similar” words it’s not bad. Million of good was classified with a modest to 8 gigabytes of memory in 1-2 minutes. You can better recognize and cluster? Naturally. There is always room for improvement.
Questions, vectorization problems and fix-heuristics
Where is the words stemmer?
Stemmer has a habit of removing prefixes, and that is what we do not need. In the same names of the goods most often the first part of the word is unchanged, although ends might be “distorted”:
- Potato young
- Potatoes young
- Young.
- Yu.
- …
No “impotatoes” and “unpotatoes” exist. And if there is, most likely it is not related to basic potatoes.
How about to use the context of the words, as it is now fashionable?
The problem is that if we consider the names of the goods, most often the words context is much more vague than in meaningful texts. For example, it is quite normal brand name – “Ladybug gold space flakes.” Marketing uses nouns and adjectives in the most perverse way, to indicate uniqueness of the goods. Thus, in this case meaningful combinations does not matter, so the context is not better than a simple count of a similar words in the names of the goods.
Words with two or more roots? If you cut a word, it becomes indistinguishable
By some luck, especially in this problem, people do not like the goods, which are named with too long words, so “Besserachtseitelesendannfunfminutenvideoseenaitung” is not at the stock (and will not be, because it is a property of a person). However, in general, this is definitely a headache that requires breaking words at the roots.
Numerals?
a) One of the problems with numbers, is that products and differ only by values. For example:
ATI Radeon 570, HDMI™ 2.0, DisplayPort 1.4 HBR3/HDR Ready
ATI Radeon 560, HDMI™ 2.0, DisplayPort 1.4 HBR3/HDR Ready
The words are the same, the numbers differ only in the second digit, and these are completely different products! In the case of IT products, it makes sense to give more weight to the numbers in function f(), because many products differs only in version. Thus, we need one more preliminary classification of goods as the goods from IT or technical field.
Another solution to this problem would be a preliminary conversion of all numerals in the words.
b) Another important issue is the unit of measurement. For example:
Shampoo, fluffy hedgehog, 1000ml.
Shampoo, fluffy hedgehog, 1 liter.
Numerals are different, and the commodities are the same. Naturally, there is one solution – to have a dictionary unit conversions. This will slow down the process, but not much.
Specificity of the clusters selection keys
Keys must break all the clusters “space” uniformly as possible in order to avoid congestion of lists with clusters elements. Otherwise, it will take too much time to search inside the list. It is required to maintain a balance between the number of keys and the sizes of the lists in the dictionary.
Author: Alexander Bespalov, Research Data Analyst, Maxilect
